

Next: 1.2.4 Variation du modèle
Up: 1.2 Le modèle numérique
Previous: 1.2.2 Modéliser les fluctuations
Revenons à notre antenne électrique immergée dans un plasma:
L'équation 1.33 et la permittivité
permet de décrire les fluctuations
électrostatiques du plasma près de la fréquence plasma,
lesquelles vont induire des courants dans l'antenne obéissant
à la loi d'Ohm, ce qu'on peut décrire formellement par
l'intermédiaire d'une
impédance d'antenne complexe 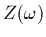 telle que
telle que 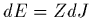 , ce qui donne, dans un plasma
isotrope
, ce qui donne, dans un plasma
isotrope
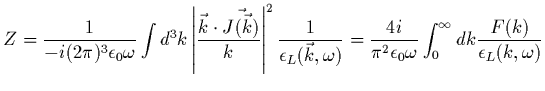 |
|
|
(1.38) |
où 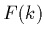 est une des réponses d'antenne (1.6) ou (1.7)
définies section 1.2.1.
est une des réponses d'antenne (1.6) ou (1.7)
définies section 1.2.1.
Finalement, dans un plasma à l'équilibre thermique à
la température T, la puissance spectrale collectée par l'antenne
d'impédance 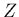 est:
est:
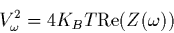 |
(1.39) |
Ce qui, compte-tenu des équations 1.36, 1.37 et 1.38 s'écrit:
où on a effectué le changement de
variable
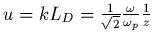 .
.
En unités SI, cela donne:
![\begin{displaymath}
V^2_\omega \simeq 8.138\,10^{-16} \sqrt{T}
\int_0^\infty \f...
...(u L/L_D) e^{-z^2} u du}{[u^2+1-\phi(z)]^2+\pi z^2
e^{-2z^2}}
\end{displaymath}](img362.gif) |
(1.42) |
où la puissance
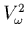 est donc exprimée en
est donc exprimée en
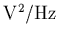 et
la température
et
la température 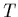 du plasma est exprimée en degrés Kelvin,
l'intégrale
du plasma est exprimée en degrés Kelvin,
l'intégrale 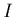 de (1.42) ne dépendant que des rapports
de (1.42) ne dépendant que des rapports
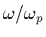 et
et 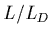 .
La difficulté du calcul numérique de cette intégrale réside
essentiellement dans
l'existence, lorsque
.
La difficulté du calcul numérique de cette intégrale réside
essentiellement dans
l'existence, lorsque
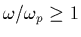 ,
de quasi pôles
,
de quasi pôles 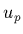 qui vérifient
qui vérifient
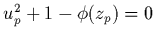 . En
approximant
. En
approximant 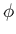 au second ordre en
au second ordre en 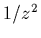 , on obtient
l'approximation de
, on obtient
l'approximation de 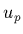 suivante (valide pour
suivante (valide pour 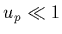 soit
soit
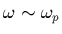 ):
):
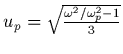 et en intégrant par résidu, on obtient la contribution
et en intégrant par résidu, on obtient la contribution 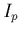 à
l'intégrale
à
l'intégrale 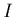 suivante:
suivante:
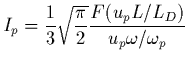 |
|
|
(1.43) |
Capacité de base du satellite et capacité d'antenne
Jusqu'ici, on s'est seulement préoccupé de calculer la ddp qui
devrait être mesuré aux bornes d'une antenne immergée dans un
plasma: bien entendu cette mesure ne peut être faite que si l'antenne est
connectée à un récepteur (généralement équipé d'un amplificateur),
lequel est monté sur une sonde spatiale. Du point de vue de
l'expérimentateur,
tout cet équipage peut être considéré comme un circuit d'impédance
finie 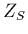 mis en parallèle aux bornes de l'antenne d'impédance
mis en parallèle aux bornes de l'antenne d'impédance 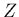 .
La puissance spectrale réellement mesurée
.
La puissance spectrale réellement mesurée 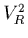 est alors:
est alors:
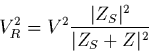 |
(1.44) |
Si la mesure est correctement calibrée et si l'instrument est bien isolé
(sans influence électromagnétique extérieure) 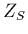 est équivalente à une capacitance
est équivalente à une capacitance
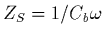 , où
, où 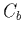 est la capacité de base de l'instrument (qui est en principe connue
avant le lancement du satellite). En notant
est la capacité de base de l'instrument (qui est en principe connue
avant le lancement du satellite). En notant 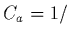 Im
Im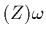 la capacité de l'antenne, (1.44) devient
la capacité de l'antenne, (1.44) devient
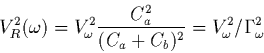 |
(1.45) |
En principe, on peut déduire la valeur exacte de 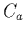 de
l'équation (1.38), ce qui donne:
de
l'équation (1.38), ce qui donne:
Mais le calcul numérique de cette intégrale est assez coûteux,
d'autant qu'elle prend l'essentiel de sa valeur pour 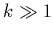 et il
faut donc prendre en compte dans le calcul de la réponse
et il
faut donc prendre en compte dans le calcul de la réponse 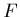 (Eqs 1.6
et 1.7) le terme
dépendant du rayon
(Eqs 1.6
et 1.7) le terme
dépendant du rayon 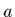 de l'antenne que l'on pouvait négliger lors du
calcul de la résistance Re(
de l'antenne que l'on pouvait négliger lors du
calcul de la résistance Re(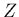 ). On peut vérifier en réalisant ce
calcul que la capacité d'antenne varie en réalité très peu avec la fréquence,
excepté très près de la fréquence plasma et peu être avantageusement
modélisée par une fonction en marche d'escalier de part et d'autre de
la fréquence plasma définie comme suit:
). On peut vérifier en réalisant ce
calcul que la capacité d'antenne varie en réalité très peu avec la fréquence,
excepté très près de la fréquence plasma et peu être avantageusement
modélisée par une fonction en marche d'escalier de part et d'autre de
la fréquence plasma définie comme suit:
La prise en compte d'une population d'électrons suprathermiques
Lorsqu'on modélise le bruit thermique avec les approximations faites
auparavant et qu'on confronte ce modèle avec par exemple un spectre radio
acquis par Ulysse dans le vent solaire -fig. 1.5- ,
on voit sur la figure que:
- le niveau de bruit
est mal modélisé en basse fréquence (
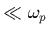 ), ce qui est dû à la
fois à la non prise en compte du bruit d'impact des particules sur
l'antenne et surtout
du bruit thermique
des protons décalé Doppler par la vitesse d'expansion du vent solaire (de
l'ordre de 400 km/s dans l'Écliptique). Pour ce dernier, nous renvoyons
le lecteur intéressé à []1.15. Pour le bruit d'impact, on peut l'estimer (en
considérant que les processus de charge de l'antenne sont uniquement
les impacts d'électrons et d'ions et les émissions
photo-électroniques) par
), ce qui est dû à la
fois à la non prise en compte du bruit d'impact des particules sur
l'antenne et surtout
du bruit thermique
des protons décalé Doppler par la vitesse d'expansion du vent solaire (de
l'ordre de 400 km/s dans l'Écliptique). Pour ce dernier, nous renvoyons
le lecteur intéressé à []1.15. Pour le bruit d'impact, on peut l'estimer (en
considérant que les processus de charge de l'antenne sont uniquement
les impacts d'électrons et d'ions et les émissions
photo-électroniques) par
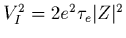 où
où 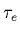 est le taux d'impact des électrons sur la surface
d'un d'antenne (d'un brin ou d'une boule). Ce taux est donné par
est le taux d'impact des électrons sur la surface
d'un d'antenne (d'un brin ou d'une boule). Ce taux est donné par
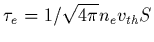 où
où 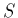 est la surface soit du brin
soit de la boule formant l'antenne.
Pour une antenne brin comme celle d'Ulysse, avec
est la surface soit du brin
soit de la boule formant l'antenne.
Pour une antenne brin comme celle d'Ulysse, avec 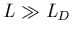 et
et
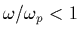 (sinon
c'est complètement négligeable) on peut en donner
l'approximation suivante:
(sinon
c'est complètement négligeable) on peut en donner
l'approximation suivante:
![\begin{displaymath}
V_I^2= V^2 4a\frac{[\ln(L_D/a)]^2}{\pi^2 L_D (\omega/\omega_p)^2}
\end{displaymath}](img401.gif) |
(1.50) |
On voit sur la figure 1.5 que cette
contribution du bruit d'impact est
de toutes façons insuffisante pour rendre compte de l'accroissement
du bruit mesuré vers les basses fréquences, lequel est en fait dominé par
le bruit décalé Doppler des protons.
- le niveau de bruit est mal modélisé pour les fréquences
supérieures a
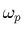 , ce qui est dû à la non prise en compte
d'une composante d'électrons «chauds» (ou suprathermiques ou de halo)
dans le vent solaire (environ 5% d'électrons 10 fois plus chauds). Nous
avons en principe les outils pour calculer la contribution de cette population:
il suffit en effet d'utiliser l'équation 1.34 pour calculer la
permittivité en tenant compte de deux populations maxwelliennes
d'électrons (core + halo) au lieu d'une. Néanmoins ce calcul double le
nombre d'intégrations et les difficultés numériques, sans changer
la nature de ces difficultés. Dans le cadre de notre projet qui doit nous
amener à ajuster le modèle aux mesures d'Ulysse
par la méthode de Levenberg-Marquardt, ce calcul double aussi le nombre de
paramètres à ajuster: c'est pourquoi
nous allons utiliser une astuce pour tenir compte de ces électrons chauds
et maintenir ainsi le nombre de paramètre à trois: la densité,
la température et un paramètre «rendant-compte» de la présence
des chauds. L'astuce repose sur la remarque suivante:
les électrons chauds ne modifient
que très peu les grandeurs caractéristiques du plasma
telles que la fréquence plasma ou la longueur de Debye (donc la
densité et la température), par contre leur
présence modifie fortement l'équation de dispersion du plasma
, ce qui est dû à la non prise en compte
d'une composante d'électrons «chauds» (ou suprathermiques ou de halo)
dans le vent solaire (environ 5% d'électrons 10 fois plus chauds). Nous
avons en principe les outils pour calculer la contribution de cette population:
il suffit en effet d'utiliser l'équation 1.34 pour calculer la
permittivité en tenant compte de deux populations maxwelliennes
d'électrons (core + halo) au lieu d'une. Néanmoins ce calcul double le
nombre d'intégrations et les difficultés numériques, sans changer
la nature de ces difficultés. Dans le cadre de notre projet qui doit nous
amener à ajuster le modèle aux mesures d'Ulysse
par la méthode de Levenberg-Marquardt, ce calcul double aussi le nombre de
paramètres à ajuster: c'est pourquoi
nous allons utiliser une astuce pour tenir compte de ces électrons chauds
et maintenir ainsi le nombre de paramètre à trois: la densité,
la température et un paramètre «rendant-compte» de la présence
des chauds. L'astuce repose sur la remarque suivante:
les électrons chauds ne modifient
que très peu les grandeurs caractéristiques du plasma
telles que la fréquence plasma ou la longueur de Debye (donc la
densité et la température), par contre leur
présence modifie fortement l'équation de dispersion du plasma
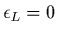 , c'est-à-dire surtout la position du pôle
, c'est-à-dire surtout la position du pôle 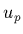 intervenant
dans le calcul de l'intégrale
intervenant
dans le calcul de l'intégrale 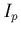 (Eq.1.43). On va faire
l'hypothèse (purement ad-hoc et un peu fausse) que les chauds
n'interviennent que de cette façon dans le bruit, et l'on va introduire
un «facteur de déplacement»
(Eq.1.43). On va faire
l'hypothèse (purement ad-hoc et un peu fausse) que les chauds
n'interviennent que de cette façon dans le bruit, et l'on va introduire
un «facteur de déplacement» 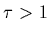 du pôle
du pôle 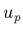 qui modifiera simplement la contribution de l'intégrale
qui modifiera simplement la contribution de l'intégrale 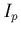 de sorte que:
de sorte que:
 |
|
|
(1.51) |
On ajustera ce paramètre 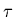 en même temps que la densité et la
température, mais on se gardera d'en donner une interprétation physique.
en même temps que la densité et la
température, mais on se gardera d'en donner une interprétation physique.
Pour résumer et conclure, le bruit thermique modélisé aux bornes de
l'antenne aura, avec les notation qui précèdent, l'expression suivante:
![\begin{displaymath}
V^2_{R}(\omega) =
\frac{8.138\,10^{-16}\sqrt{T}}{\Gamma^{2}...
...{[u^2+1-\phi(z)]^2+\pi z^2
e^{-2z^2}} + I_{p} \right] + V_I^2
\end{displaymath}](img408.gif) |
(1.52) |
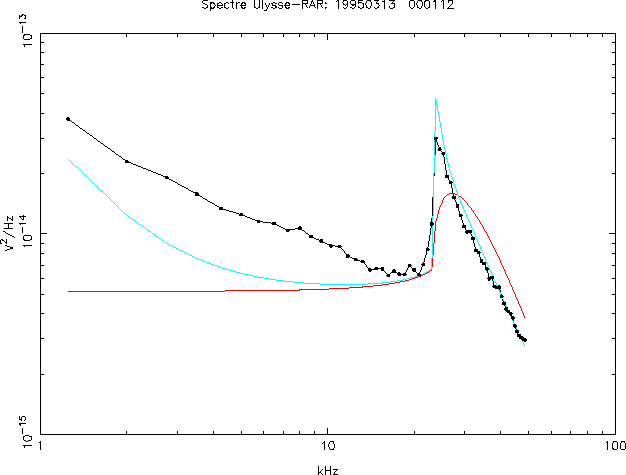
Figure 1.5:
Spectre basse fréquence obtenu par Ulysse dans le vent
solaire. Les points reliés par des lignes blanches sont les mesures en
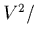 Hz de la puissance collecté par l'antenne S pour chacun des 64
paliers de fréquence. La courbe rouge est un modèle de spectre
calculé pour
Hz de la puissance collecté par l'antenne S pour chacun des 64
paliers de fréquence. La courbe rouge est un modèle de spectre
calculé pour 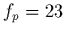 kHz et
kHz et 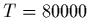 K, tenant dompte de la capacitance
de l'instrument, mais calculé sans tenir compte ni du bruit
d'impact (
K, tenant dompte de la capacitance
de l'instrument, mais calculé sans tenir compte ni du bruit
d'impact (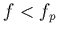 ), ni de la présence d'un halo d'électrons chauds
(
), ni de la présence d'un halo d'électrons chauds
(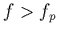 ). La courbe
bleue en tient compte comme expliqué ci-dessus
(Rq: aucun modèle
représenté ici ne tient compte du bruit protonique décalé Doppler)
). La courbe
bleue en tient compte comme expliqué ci-dessus
(Rq: aucun modèle
représenté ici ne tient compte du bruit protonique décalé Doppler)
 |


Next: 1.2.4 Variation du modèle
Up: 1.2 Le modèle numérique
Previous: 1.2.2 Modéliser les fluctuations
Michel Moncuquet
DESPA, Observatoire de Paris
2001-03-05
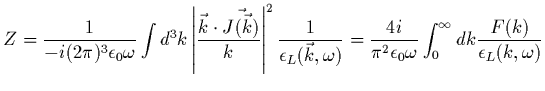
![]() est:
est:
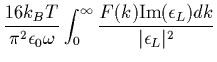
![$\displaystyle \frac{8\sqrt{2 m_e K_B}}{\pi^{3/2}\epsilon_0} \sqrt{T}
\int_0^\infty \frac{F(uL/L_D) e^{-z^2} u du}{[u^2+1-\phi(z)]^2+\pi z^2 e^{-2z^2}}$](img360.gif)
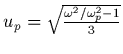 et en intégrant par résidu, on obtient la contribution
et en intégrant par résidu, on obtient la contribution ![]() mis en parallèle aux bornes de l'antenne d'impédance
mis en parallèle aux bornes de l'antenne d'impédance ![]() .
La puissance spectrale réellement mesurée
.
La puissance spectrale réellement mesurée ![]() est alors:
est alors:
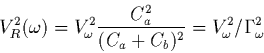
![]() de
l'équation (1.38), ce qui donne:
de
l'équation (1.38), ce qui donne:
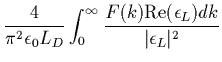
![$\displaystyle \frac{4}{\pi^2 \epsilon_0 L_{D}}
\int_0^\infty \frac{F(uL/L_D) [u^2+1-\phi(z)] u^{2} du}
{[u^2+1-\phi(z)]^2+\pi z^2 e^{-2z^2}}$](img388.gif)
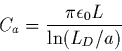
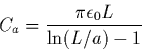
![\begin{displaymath}
V_I^2= V^2 4a\frac{[\ln(L_D/a)]^2}{\pi^2 L_D (\omega/\omega_p)^2}
\end{displaymath}](img401.gif)

