

Next: Ajustement d'un modèle aux
Up: 1.2 Le modèle numérique
Previous: 1.2.3 L'impédance d'antenne et
Pour mettre en ÷uvre la méthode de Levenberg-Marquardt -qui recherche
le minimum du 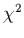 par ajustement de paramètres choisis- il est
nécessaire de savoir calculer les dérivées partielles du modèle par rapport
aux paramètres à ajuster -ici
par ajustement de paramètres choisis- il est
nécessaire de savoir calculer les dérivées partielles du modèle par rapport
aux paramètres à ajuster -ici 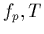 et
et 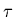 . Ces calculs
sont sans mystère mais fastidieux 1.16 et consistent à dériver par rapport
à chacun des paramètres d'ajustement l'expression (1.52) (en négligeant ici
le bruit d'impact
. Ces calculs
sont sans mystère mais fastidieux 1.16 et consistent à dériver par rapport
à chacun des paramètres d'ajustement l'expression (1.52) (en négligeant ici
le bruit d'impact 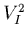 puisqu'on ne modélise de toutes façons pas
le bruit des
protons qui est dominant aux basses fréquences) 1.17.
Par rapport à la température T des électrons, on obtient:
puisqu'on ne modélise de toutes façons pas
le bruit des
protons qui est dominant aux basses fréquences) 1.17.
Par rapport à la température T des électrons, on obtient:
![$\displaystyle \frac{\partial V^2_{R}}{\partial T} =
\frac{ 8.138\,10^{-16} }{2\...
...L/L_D) e^{-z^2} u^{2} du}
{[u^2+1-\phi(z)]^2+\pi z^2 e^{-2z^2}} \right. \right.$](img413.gif) |
|
|
|
![$\displaystyle \left. \left. + \sqrt{\frac{\pi}{18}} \frac{\tau F'(\tau u_{p}
L/L_D)}{(\omega/\omega_{p})^{1/\tau^2}} \right]
\right)$](img414.gif) |
|
|
(1.53) |
avec ici:
-si
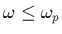 :
:
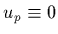 et
et
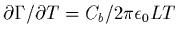
-si
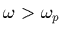 :
:
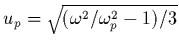 et
et
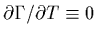 ,
,
et
où 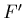 désigne la dérivée de la réponse d'antenne
désigne la dérivée de la réponse d'antenne 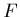 ;
dans le cas d'une antenne filaire, on aura:
;
dans le cas d'une antenne filaire, on aura:
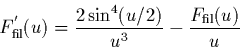 |
(1.54) |
Par rapport au paramètre ad-hoc 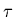 , on aura:
, on aura:
![\begin{displaymath}
\frac{\partial V^2_{R}}{\partial \tau} =
\frac{8.138\,10^{-...
...mega/\omega_{p})}{\tau^{3}}F(\tau u_{p} \frac{L}{L_D}) \right]
\end{displaymath}](img422.gif) |
(1.55) |
avec les mêmes conditions vis-à-vis du rapport
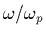 qu'en (1.53).
qu'en (1.53).
Enfin, pour dériver (1.52) par rapport à 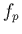 , le calcul
explicite est difficile et coûteux (mêmes difficultés que pour le calcul
de capacitance). On utilisera donc une méthode de
dérivation numérique, telle que la méthode de Ridders-Richardson, ou
une interpolation polynomiale suivie d'une dérivation algébrique, avec les
précautions requises lors du choix du "pas de calcul" dans le premier
cas1.18,
ou lors du choix judicieux du polynôme d'interpolation dans le
second cas1.19.
, le calcul
explicite est difficile et coûteux (mêmes difficultés que pour le calcul
de capacitance). On utilisera donc une méthode de
dérivation numérique, telle que la méthode de Ridders-Richardson, ou
une interpolation polynomiale suivie d'une dérivation algébrique, avec les
précautions requises lors du choix du "pas de calcul" dans le premier
cas1.18,
ou lors du choix judicieux du polynôme d'interpolation dans le
second cas1.19.
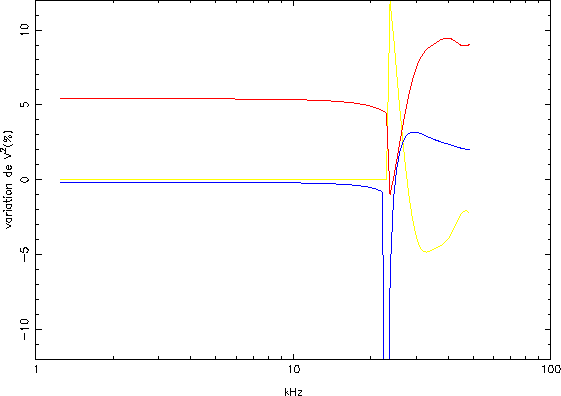
Figure 1.6:
Variation relative du bruit thermique 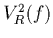 sur
Ulysse obtenue par le calcul des dérivées partielles logarithmiques de
sur
Ulysse obtenue par le calcul des dérivées partielles logarithmiques de
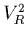 par rapport à
par rapport à 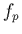 (ligne bleue),
(ligne bleue), 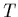 (ligne rouge) et
accessoirement
(ligne rouge) et
accessoirement 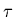 (ligne jaune).
Ces variations sont ici calculées pour les valeurs
des paramètres suivantes:
(ligne jaune).
Ces variations sont ici calculées pour les valeurs
des paramètres suivantes:
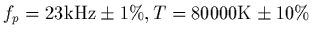 et
et
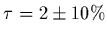
 |


Next: Ajustement d'un modèle aux
Up: 1.2 Le modèle numérique
Previous: 1.2.3 L'impédance d'antenne et
Michel Moncuquet
DESPA, Observatoire de Paris
2001-03-05
![$\displaystyle \frac{\partial V^2_{R}}{\partial T} =
\frac{ 8.138\,10^{-16} }{2\...
...L/L_D) e^{-z^2} u^{2} du}
{[u^2+1-\phi(z)]^2+\pi z^2 e^{-2z^2}} \right. \right.$](img413.gif)
![$\displaystyle \left. \left. + \sqrt{\frac{\pi}{18}} \frac{\tau F'(\tau u_{p}
L/L_D)}{(\omega/\omega_{p})^{1/\tau^2}} \right]
\right)$](img414.gif)
![]() , le calcul
explicite est difficile et coûteux (mêmes difficultés que pour le calcul
de capacitance). On utilisera donc une méthode de
dérivation numérique, telle que la méthode de Ridders-Richardson, ou
une interpolation polynomiale suivie d'une dérivation algébrique, avec les
précautions requises lors du choix du "pas de calcul" dans le premier
cas1.18,
ou lors du choix judicieux du polynôme d'interpolation dans le
second cas1.19.
, le calcul
explicite est difficile et coûteux (mêmes difficultés que pour le calcul
de capacitance). On utilisera donc une méthode de
dérivation numérique, telle que la méthode de Ridders-Richardson, ou
une interpolation polynomiale suivie d'une dérivation algébrique, avec les
précautions requises lors du choix du "pas de calcul" dans le premier
cas1.18,
ou lors du choix judicieux du polynôme d'interpolation dans le
second cas1.19.
