APPENDIX

Consider a distribution made of a sum of Maxwellians of temperatures and densities , at z = 0. Eq.(4) shows that the distribution at distance z is a sum of Maxwellians of temperatures and densities

The temperature of each individual Maxwellian (which, as seen in Sect.4, is independent of q and z) is related to its moment by Eq.(6), i.e.

where, by definition, . The temperature of the whole distribution at distance z is obtained by substituting in (6) its moment with the above expressions of . This gives

To find the sense of variation of , we have to calculate the sign of the derivative :

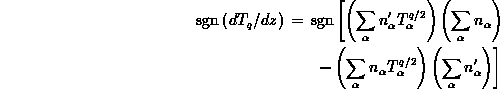
where

Thus

 

The bracket can be rearranged by dropping the terms that cancel out in the summations, and symmetrizing over the dummy indices. This gives:

which is a sum of positive terms, so that the bracket in Eq.( 31) is positive. Hence, with a monotonic attractive potential ( ), the temperatures all increase with z. This holds for a velocity distribution which can be modelled by a sum of several Maxwellians (a single Maxwellian giving ).

Acknowledgements

The Ulysses URAP experiment, whose Principal Investigator is R.G. Stone, is a joint project of NASA/GSFC, Observatoire de Paris, CRPE and University of Minnesota. The French contribution was mainly financed by the CNES. We are very grateful to the team at the Département de Recherche Spatiale (Observatoire de Paris), who designed, built and tested the radio astronomy receivers, whose great performances allowed us to obtain these results. We thank our colleagues at GSFC for the successful operation of the experiment during the flyby and their help in the data reduction. We thank D. F. Strobel for his critical reading of an earlier version of this paper and useful suggestions, the referees for their helpful comments, and J. L. Steinberg for his suggestions which made this paper easier to understand.