SUMMARY AND FINAL REMARKS

Our main results are:

1. The electron density and the effective temperature in the outer Io torus are anticorrelated, following an approximate polytrope law of exponent 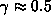. They were measured in situ aboard Ulysses, along a trajectory which crossed the equator basically north-to-south around 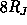from Jupiter.
2. This can be explained by the filtration of velocities ([Scudder 1992a]) by the potential which confines the particles to the equator, and thus behaves as a high-pass velocity filter for non-Maxwellian distributions. The polytrope exponent 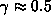is obtained with an electron velocity distribution which can be approximated by a Kappa function with 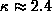, approaching a Maxwellian at low and thermal energies and joining to a power-law ( 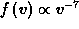) at high energies.
3. Our measurements cannot be explained by the usual quasi-thermal model where the electron distribution is made of a Maxwellian plus a Maxwellian tail (isotropic or not). Due to their larger free paths, the ions are even less thermalized than the electrons; this suggests that velocity filtration is as least as effective for the ions, so that they should not be described as fluid species with constant temperatures.
4. Assuming a single isotropic ion species, we have deduced a simple theoretical density profile, whose variation with latitude is Kappa-like instead of the classical (isothermal) Gaussian. This calculated profile fits quite well our measured densities. This profile arises as a direct consequence of Kappa velocity distributions (which have suprathermal tails), just as the Gaussian profile derives from the Maxwellian assumption; it can also be derived from the fluid equations closed with the observed polytrope law, just as the Gaussian can be derived from the fluid equations with a constant temperature. Farther than a scale-height, the Kappa-like profile decreases much more slowly than the Gaussian, since the supra-thermal tail is less equatorially confined. Contrary to the traditional density profiles based on Maxwellian distribution functions for all particle species, the Kappa-like density decrease along field lines is power-law farther than a scale-height.

The present model is admittedly very crude, since it assumes a single ion species, neglects particle anisotropies and magnetic field variations, considers very simple distribution functions, and ignores temporal and longitudinal variations. It is aimed at explaining the basic trends of our observations, and illustrating in the Io torus the physics implied by the absence of local thermal equilibrium: the temperature(s) increase(s) with latitude, and the density profile is very sensitive to the shape of the particle velocity distributions. It is important to note that our main result (the polytrope relation between 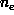and and its interpretation) only depends on the electron velocity distribution; it is of course unaffected by the number of ion species, their distributions, and the anisotropies (in the latitude range considered). This leads us to suggest that the traditional assumption of constant temperatures along field lines is expected to be inadequate in the outer torus, and should be relaxed in future detailed models.

We have focused here on the smooth variations of the parameters. In the close vicinity of the magnetic equator, we also observed variations over a scale smaller than a few degrees in latitude and/or longitude (Fig.1), which seem to follow a similar polytropic law. But we have not tried to interpret them, because the instrument temporal resolution (128 s) makes it difficult to resolve the large gradients involved.