

Next: 2.3 Modèles non-linéaires: Méthode
Up: 2.2 Modèles linéaires et
Previous: 2.2.1.1 Régression linéaire avec
2.2.2 Modèles linéaires à M paramètres
Une généralisation immédiate de la régression linéaire, consiste à
considérer, au lieu d'une simple droite affine 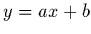 , un modèle
formé d'une combinaison linéaire de
, un modèle
formé d'une combinaison linéaire de 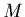 fonctions de
fonctions de 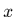 . Par exemple,
ces fonctions peuvent être
. Par exemple,
ces fonctions peuvent être
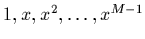 , auquel cas leur
combinaison linéaire sont les polynômes de degré
, auquel cas leur
combinaison linéaire sont les polynômes de degré 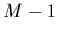 . La forme
générale de ces modèles est
. La forme
générale de ces modèles est
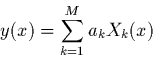 |
(2.18) |
où
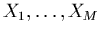 sont des fonctions2.4
de
sont des fonctions2.4
de 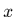 appelées fonctions de base.
appelées fonctions de base.
Pour ces modèles linéaires on va généraliser tout ce qui a été
dit section 2.2.1. Pour commencer, le chi-carré s'écrit dans ce
cas:
![\begin{displaymath}
\chi^{2}= \sum_{i=1}^{N}\left[ \frac{y_{i}-\sum_{k=1}^M a_k X_k(x_i)}
{\sigma_{i}}\right]^{2}
\end{displaymath}](img492.gif) |
(2.19) |
D'autre part, et comme dans le cas de la régression, viser le minimum de ce
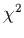 va aboutir à la résolution d'un système
linéaire, mais cette fois de
va aboutir à la résolution d'un système
linéaire, mais cette fois de 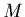 équations
à
équations
à 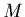 inconnues:
inconnues:
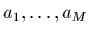 . Pour obtenir ce système, il suffit
d'écrire que les dérivées partielles du
. Pour obtenir ce système, il suffit
d'écrire que les dérivées partielles du 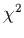 par rapport
au paramètres
par rapport
au paramètres
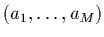 (i.e. le gradient du
(i.e. le gradient du 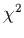 ) s'annulent
au minimum, soit:
) s'annulent
au minimum, soit:
Ces équations sont appelées système d'équations normales
de la méthode du chi-carré.
Pour mieux formaliser ce système linéaire, il nous faut introduire
quelques notations matricielles et vectorielles: soit A la matrice 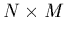 (dite "matrice modèle") dont les composantes sont définies par:
(dite "matrice modèle") dont les composantes sont définies par:
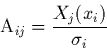 |
(2.21) |
Remarquons que le terme
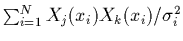 , qui
apparaît lorsqu'on échange l'ordre des sommations dans (2.20), est
la composante d'indice
, qui
apparaît lorsqu'on échange l'ordre des sommations dans (2.20), est
la composante d'indice 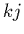 d'une matrice carrée
d'une matrice carrée 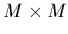 qui n'est autre
que
qui n'est autre
que
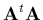 , où
, où 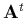 désigne la transposée de
désigne la transposée de 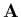 . Définissons aussi un vecteur
. Définissons aussi un vecteur 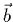 à
à 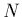 composantes par
composantes par
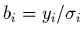 et posons enfin les paramètres à ajuster sous
forme d'un vecteur à
et posons enfin les paramètres à ajuster sous
forme d'un vecteur à 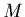 composantes :
composantes :
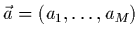 .
Avec ces notations, le système (2.20) s'écrit:
.
Avec ces notations, le système (2.20) s'écrit:
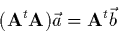 |
(2.22) |
D'un point de vue numérique, il suffit donc de résoudre le système
(2.22) par une méthode bien adaptée2.5 mais on
préférera une méthode qui calcule explicitement la matrice inverse de
la matrice
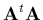 car, comme on va le voir maintenant, cette
matrice
car, comme on va le voir maintenant, cette
matrice
![${\bf C}=[ {\bf A}^t{\bf A} ]^{-1}$](img510.gif) , dite matrice de covariance,
va nous permettre d'estimer les incertitudes (les écart-types) sur les
paramètres ajustés.
, dite matrice de covariance,
va nous permettre d'estimer les incertitudes (les écart-types) sur les
paramètres ajustés.
Écart-type sur les paramètres ajustés
En utilisant la matrice de covariance,
le système (2.22) s'écrit
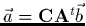 ,
soit en composantes:
,
soit en composantes:
![\begin{displaymath}
a_j=\sum_{k=1}^M {\rm C}_{jk}\left[\sum_{i=1}^M \frac{y_i X_k(x_i)}{\sigma_i^2}
\right]
\end{displaymath}](img512.gif) |
(2.23) |
ce qui nous permet de calculer les dérivées partielles
d'un paramètre ajusté 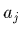 par rapport
aux
par rapport
aux 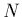 mesures indépendantes
mesures indépendantes 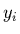 :
:
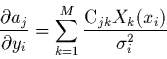 |
(2.24) |
et la relation (2.14) s'écrit dans ce cas
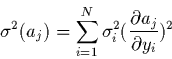 |
(2.25) |
Ce qui aboutit finalement à:
![\begin{displaymath}
\sigma^2(a_j)=\sum_{k=1}^M \sum_{l=1}^M {\rm C}_{jk}{\rm C}_...
...^2} \right]
= [{\bf C}^2 {\bf A}^t{\bf A}]_{jj} = {\rm C}_{jj}
\end{displaymath}](img516.gif) |
(2.26) |
Autrement dit, les éléments diagonaux de 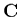 sont les variances
-les carrés des écart-types- sur chacun des paramètres ajustés
sont les variances
-les carrés des écart-types- sur chacun des paramètres ajustés 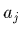 .
Les éléments
non-diagonaux
.
Les éléments
non-diagonaux
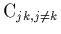 sont les covariances entre les
paramètres
sont les covariances entre les
paramètres 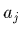 et
et 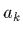 et permettent d'apprécier l'ajustement par
rapport aux variations conjointes des deux paramètres.
et permettent d'apprécier l'ajustement par
rapport aux variations conjointes des deux paramètres.


Next: 2.3 Modèles non-linéaires: Méthode
Up: 2.2 Modèles linéaires et
Previous: 2.2.1.1 Régression linéaire avec
Michel Moncuquet
DESPA, Observatoire de Paris
2001-03-05
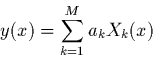
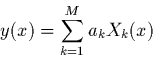
![\begin{displaymath}
\chi^{2}= \sum_{i=1}^{N}\left[ \frac{y_{i}-\sum_{k=1}^M a_k X_k(x_i)}
{\sigma_{i}}\right]^{2}
\end{displaymath}](img492.gif)
![]() (dite "matrice modèle") dont les composantes sont définies par:
(dite "matrice modèle") dont les composantes sont définies par:
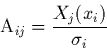
![]() car, comme on va le voir maintenant, cette
matrice
car, comme on va le voir maintenant, cette
matrice
![]() , dite matrice de covariance,
va nous permettre d'estimer les incertitudes (les écart-types) sur les
paramètres ajustés.
, dite matrice de covariance,
va nous permettre d'estimer les incertitudes (les écart-types) sur les
paramètres ajustés.
![]() ,
soit en composantes:
,
soit en composantes:
![\begin{displaymath}
a_j=\sum_{k=1}^M {\rm C}_{jk}\left[\sum_{i=1}^M \frac{y_i X_k(x_i)}{\sigma_i^2}
\right]
\end{displaymath}](img512.gif)
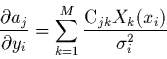
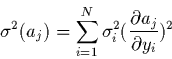
![\begin{displaymath}
\sigma^2(a_j)=\sum_{k=1}^M \sum_{l=1}^M {\rm C}_{jk}{\rm C}_...
...^2} \right]
= [{\bf C}^2 {\bf A}^t{\bf A}]_{jj} = {\rm C}_{jj}
\end{displaymath}](img516.gif)
![]() sont les variances
-les carrés des écart-types- sur chacun des paramètres ajustés
sont les variances
-les carrés des écart-types- sur chacun des paramètres ajustés ![]() .
Les éléments
non-diagonaux
.
Les éléments
non-diagonaux
![]() sont les covariances entre les
paramètres
sont les covariances entre les
paramètres ![]() et
et ![]() et permettent d'apprécier l'ajustement par
rapport aux variations conjointes des deux paramètres.
et permettent d'apprécier l'ajustement par
rapport aux variations conjointes des deux paramètres.