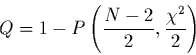

Next: 2.2.1.1 Régression linéaire avec
Up: 2.2 Modèles linéaires et
Previous: 2.2 Modèles linéaires et
2.2.1 Régression linéaire
La terminologie "régression linéaire" est historique et provient des
premiers travaux statistiques en sciences sociales. En théorie, il s'agit de
déterminer la droite du plan affine qui s'ajuste au mieux à un un
ensemble de 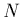 points de mesure
points de mesure 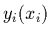 . Autrement dit, en supposant
que les erreurs de mesures sont distribuées normalement par rapport à
une droite, on cherchera à ajuster au moindre
. Autrement dit, en supposant
que les erreurs de mesures sont distribuées normalement par rapport à
une droite, on cherchera à ajuster au moindre 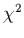 le modèle
linéaire à 2 paramètres
le modèle
linéaire à 2 paramètres 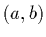 :
: 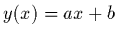 , où
, où 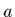 est donc
la pente et
est donc
la pente et 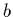 l'ordonnée à l'origine de la droite recherchée (dite
de régression).
L'expression du
l'ordonnée à l'origine de la droite recherchée (dite
de régression).
L'expression du 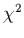 se réduit dans ce cas à
se réduit dans ce cas à
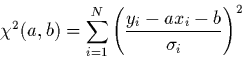 |
(2.9) |
et le 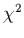 sera minimum lorsque ses dérivées partielles par
rapport à
sera minimum lorsque ses dérivées partielles par
rapport à 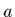 et
et 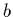 seront nulles:
seront nulles:
en posant génériquement pour tout couple de 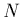 -uplet
-uplet
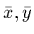
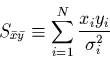 |
(2.11) |
et en posant, pour simplifier les notations,
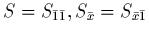 , le système (2.10) s'écrit
, le système (2.10) s'écrit
et posant
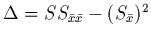 , la solution
de (2.10) est:
, la solution
de (2.10) est:
Incertitudes sur les paramètres de régression, confiance
L'équation (2.13) nous donne donc la pente 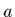 et l'ordonnée à l'origine
et l'ordonnée à l'origine
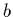 de la droite de régression, mais
il nous reste maintenant à estimer les incertitudes sur ces paramètres
ajustés, puisque l'existence d'erreurs sur les mesures doit évidemment
introduire une incertitude sur la détermination de
de la droite de régression, mais
il nous reste maintenant à estimer les incertitudes sur ces paramètres
ajustés, puisque l'existence d'erreurs sur les mesures doit évidemment
introduire une incertitude sur la détermination de 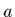 et
et 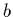 (notons
au passage que cette question se posera dans tous les problèmes
d'ajustement, et ceci quel que soit le nombre de
paramètres ajustés et que le modèle en dépende linéairement ou
non). Puisque les mesures d'un point à un autre sont indépendantes et
que la variance de toute fonction
(notons
au passage que cette question se posera dans tous les problèmes
d'ajustement, et ceci quel que soit le nombre de
paramètres ajustés et que le modèle en dépende linéairement ou
non). Puisque les mesures d'un point à un autre sont indépendantes et
que la variance de toute fonction 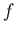 définie sur
définie sur 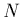 mesures indépendantes vérifie la relation:
mesures indépendantes vérifie la relation:
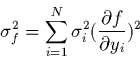 |
(2.14) |
on pourra appliquer cette relation aux paramètres 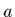 et
et 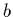 .
.
En calculant les dérivées partielles de 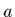 et
et 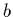 par
rapport à
par
rapport à 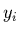 grâce à (2.13), on en déduit finalement
grâce à (2.13), on en déduit finalement
Nous n'avons pas tout-à-fait terminé:
nous devons estimer la critère de confiance de l'ajustement
donné par l'équation (2.6),
qui dans ce cas va indiquer la probabilité
que la droite de régression obtenue n'est pas fortuite et se réduit à
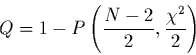 |
(2.17) |
Donnons pour ce critère quelques limites empiriques mais pratiques: si 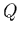 est plus grand que 0.1, l'ajustement est crédible; si
est plus grand que 0.1, l'ajustement est crédible; si 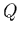 est plus grand
que -disons 0.001-, il faut voir: l'ajustement est peut-être acceptable si
les erreurs ont été modérément sous-estimées ou peut-être
suffit-il d'exclure quelques points aberrants. Enfin, si
est plus grand
que -disons 0.001-, il faut voir: l'ajustement est peut-être acceptable si
les erreurs ont été modérément sous-estimées ou peut-être
suffit-il d'exclure quelques points aberrants. Enfin, si 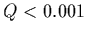 , soit un
modèle de régression est inadapté, soit il faut avoir recours à
une méthode robuste mais pas à un ajustement aux moindres carrés
(ce sera notamment le cas s'il y a beaucoup de points aberrants).
, soit un
modèle de régression est inadapté, soit il faut avoir recours à
une méthode robuste mais pas à un ajustement aux moindres carrés
(ce sera notamment le cas s'il y a beaucoup de points aberrants).
Sous-sections


Next: 2.2.1.1 Régression linéaire avec
Up: 2.2 Modèles linéaires et
Previous: 2.2 Modèles linéaires et
Michel Moncuquet
DESPA, Observatoire de Paris
2001-03-05
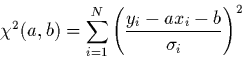
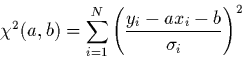
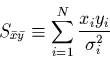
![]() et l'ordonnée à l'origine
et l'ordonnée à l'origine
![]() de la droite de régression, mais
il nous reste maintenant à estimer les incertitudes sur ces paramètres
ajustés, puisque l'existence d'erreurs sur les mesures doit évidemment
introduire une incertitude sur la détermination de
de la droite de régression, mais
il nous reste maintenant à estimer les incertitudes sur ces paramètres
ajustés, puisque l'existence d'erreurs sur les mesures doit évidemment
introduire une incertitude sur la détermination de ![]() et
et ![]() (notons
au passage que cette question se posera dans tous les problèmes
d'ajustement, et ceci quel que soit le nombre de
paramètres ajustés et que le modèle en dépende linéairement ou
non). Puisque les mesures d'un point à un autre sont indépendantes et
que la variance de toute fonction
(notons
au passage que cette question se posera dans tous les problèmes
d'ajustement, et ceci quel que soit le nombre de
paramètres ajustés et que le modèle en dépende linéairement ou
non). Puisque les mesures d'un point à un autre sont indépendantes et
que la variance de toute fonction ![]() définie sur
définie sur ![]() mesures indépendantes vérifie la relation:
mesures indépendantes vérifie la relation:
![]() et
et ![]() par
rapport à
par
rapport à ![]() grâce à (2.13), on en déduit finalement
grâce à (2.13), on en déduit finalement