Instead of a superposition of a several Maxwellians, let us consider the simpler non-thermal distribution:
This generalized Lorentzian function is
very convenient to model observed velocity distributions
([Vasyliunas 1968]), since it is quasi-Maxwellian at low and thermal
energies, while its non-thermal tail decreases as a power-law
at high energies, as generally observed in space plasmas; this is in
line with the fact that particles of higher energy have larger
free paths, and are thus less likely to achieve partial
equilibrium. A generating process for such distributions has
been suggested recently ([Collier 1993]). For typical space plasmas,
generally lies in the range 2-6.
This ``Kappa" distribution tends to a Maxwellian for 
since
In this limit, all the temperatures 
.
For
finite , however, the temperatures 
are different and
increase with q. In particular the traditional temperature is
and the effective temperature 
is
The larger , the closer the distribution is to a Maxwellian,
and the closer the 's are to 
.
Substituting (10) into (4), one
sees that the
distribution at distance z is still a Kappa function having the
same . In addition, as a consequence of the form (10),
we have
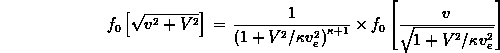
Substituting this relationship into the integral (6) and
changing variables
to recover 
in the integrand, we get
(with 
, in order that the integrals converge). Since
the density is the moment of order q = 0, this yields
Thus 
, and, since
, we deduce
The 's and 
thus follow a polytrope law, which is independent
of q. This generalizes the result of Scudder (1992a) to all the
temperatures , and in particular to the temperature 
given by our measurement.
Hence with a Kappa distribution, the density and temperature obey a polytrope law, not only when the temperature is defined from the mean particle energy, but also when it is based on other moments of the distribution, a situation encountered with some measuring techniques.
