Let us study the relation between 
and 
. We only
consider the region from +15 to 
centrifugal latitude, where
the and measurements are independent and the uncertainties
rather small. Fig. 2 shows the data plotted as temperature
versus density in a log-log format, and the associated best-fit
line. Since it would be inadequate to determine the slope from a classical
linear least-squares fitting, because of the finite errors bars on
both and , we used a standard (non-linear) approach taking
into account the uncertainties on both variables ([Press et al. 1992]); to calculate the 
merit function,
the square deviations between measurements and model are weighted
by 
, where 
and 
are the measurement
uncertainties and 
the slope to
be determined,
in log-log coordinates. This yields the polytrope relation
with 
(3 
).
The correlation coefficient between and is r =
-0.87.
Given the number of data points (46), the level of significance
of that anticorrelation is very high.
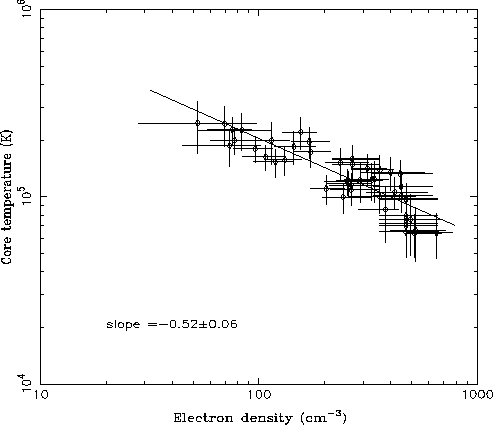
Figure 2: Electron parameters measured in situ aboard
Ulysses, plotted as temperature versus density, and the associated best-fit
line. The data span 
in latitudinal distance. (The longitude
varies by 
, centered near 
, and
the Jovicentric distance only varies from 7.1 to 8.4 
. We have used the
data plotted with solid error bars in Fig.1, which are independent
measurements of and .)
