To calculate explicitly the density profile of Eq.(15),
we must first calculate the electric potential 
.
As usual,
one has to calculate the ion density profiles, and then to impose
charge quasi-neutrality. In the frame of the microscopic
formulation considered above, this requires the knowledge of the ion
velocity distributions at z = 0.
Unfortunately, the ion velocity distributions in the torus
were not measured aboard Ulysses. They could not be
unambiguously determined from Voyager measurements either, because,
among other problems, the spectra of individual ion species could
not be resolved. Nevertheless, the data indicated that the
velocity distributions were not Maxwellian in the corotating
frame ([Bagenal and Sullivan 1981]; [Bagenal 1989]). Likewise, theoretical
models imply
highly non-thermal distributions ([Richardson and Siscoe 1983]; [Smith and Strobel 1985]).
In the
spirit of the simple illustrative model considered here, we
will assume that there is only one ion species of mass 
and charge
Ze,
and model its non-Maxwellian distribution by a Kappa
function having the same 
as the electrons. This is certainly
oversimplified, and in particular the values of need not be
equal for ions and electrons. However, our aim is not to build a detailed
empirical model (which would have a large number of unknown
parameters since the distributions of individual ion species are
poorly known), but rather to explore the consequences of
non-Maxwellian distributions. In this context, the Kappa
distribution is the simplest choice retaining the basic shape of
the measured velocity distributions, which are not too far from
Maxwellians at low energies but have power-law supra-thermal
tails.
So we take for the ion distribution
The centrifugal force (3) derives from the potential
(for 
). The ions are thus subjected to the total potential
. As can be verified a posteriori,
this potential
attracts them monotonically (as 
does for the electrons), so
that their density profile is given by replacing in the
expression (15) of the electron profile `` 
" by
`` 
", and 
by 
. Since
charge neutrality
requires that 
, the
electron and ion densities
should be proportional to each other, which requires
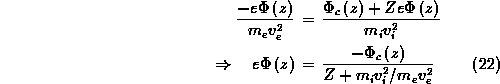
Substituting into (15) with the expression (21)
of 
, one obtains finally
which is a slightly modified Kappa function. Not unexpectedly, the
latitudinal density profile reflects the behaviour of the
velocity distributions. Note that H can be expressed as a
function of the
particle mean random energies at z = 0, i.e., of the
classical temperatures (12) at z = 0, which we denote
by 
and 
for respectively the electrons and the ions; this gives
