

Next: 0.3.2 Élasticité linéaire isotrope
Up: 0.3 Élasticité linéaire
Previous: 0.3 Élasticité linéaire
Lorsqu'on cherche à définir la notion de déformation d'un milieu
continu, ce concept est différent, selon qu'on peut introduire la notion
de vitesse des particules qui forment le milieu
(cas des fluides) ou lorsqu'on ne dispose
que de la notion de déplacement par rapport à une position initiale
privilégiée (cas des solides déformables). Dans le premier cas, on peut caractériser de façon
naturelle la vitesse de déformation par un tenseur qui s'exprime en
fonction de la vitesse d'une particule par
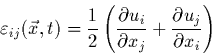 |
(39) |
Dans le cas des solides déformables,
on montre facilement que la déformation peut être caractérisée par un
champ de tenseur, dit de Green-Lagrange, qui s'exprime de façon
non-linéaire par rapport aux dérivées partielles du déplacement.
Cependant, pour les milieux solides, les déplacements varient très
lentement lorsqu'on passe de l'état initial à l'état déformé : on peut
alors négliger les termes non-linéaires (quadratiques) du tenseur de
Green-Lagrange et obtenir un tenseur des déformations linéarisées qui,
considéré comme un opérateur différentiel sur le champ des
déplacements a exactement la même expression que le tenseur des
vitesses de déformation opérant sur le champ des vitesses en
mécanique des fluides. Autrement dit, pour un solide se déformant
lentement, le
tenseur des déformations est donné par l'équation (39) avec
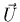 représentant le champ des déplacements par rapport à l'état
initial du solide.
représentant le champ des déplacements par rapport à l'état
initial du solide.
Comme dans le cas d'un fluide visqueux, on aura à écrire a priori la
conservation de la masse et de la quantité de mouvement, mais sous
l'hypothèse de petites perturbations, la divergence des
déplacements est très petite et la conservation de la masse se
réduit alors approximativement
à la conservation de la masse volumique du solide lors de
sa déformation
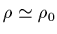 . Compte tenu que
. Compte tenu que 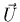 est
un champ de déplacement, la conservation de la quantité de mouvement
s'écrit:
est
un champ de déplacement, la conservation de la quantité de mouvement
s'écrit:
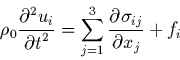 |
(40) |
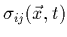 sont les composantes du tenseur
symétrique des contraintes.
sont les composantes du tenseur
symétrique des contraintes.
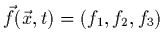 est la densité volumique des
forces extérieures agissant sur le solide (généralement les forces de
pesanteur)
est la densité volumique des
forces extérieures agissant sur le solide (généralement les forces de
pesanteur)


Next: 0.3.2 Élasticité linéaire isotrope
Up: 0.3 Élasticité linéaire
Previous: 0.3 Élasticité linéaire
Michel Moncuquet
DESPA, Observatoire de Paris
2001-03-05
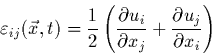
![]() . Compte tenu que
. Compte tenu que ![]() est
un champ de déplacement, la conservation de la quantité de mouvement
s'écrit:
est
un champ de déplacement, la conservation de la quantité de mouvement
s'écrit: