

Next: 0.3 Élasticité linéaire
Up: 0.2 Transmission de la
Previous: 0.2.2 Conservation de l'énergie
On cherche à généraliser la loi de comportement (3)
pour qu'elle rende également compte de la relation
entre les contraintes et les caractéristiques thermodynamiques du fluide,
comme le flux de chaleur et la température. On va le faire en
caractérisant la diffusion de l'énergie dans le milieu due aux effets
(supposés découplés)
de la viscosité du fluide et de la conduction thermique du fluide.
Dans la loi de comportement
(3) le terme
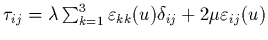 représente les contraintes visqueuses et
aboutit, via l'équation de conservation de l'énergie (30), à définir
une diffusion d'énergie d'origine purement mécanique
représente les contraintes visqueuses et
aboutit, via l'équation de conservation de l'énergie (30), à définir
une diffusion d'énergie d'origine purement mécanique
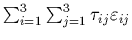 dite de
dissipation visqueuse.
dite de
dissipation visqueuse.
Pour préciser le terme de dissipation thermique, on adopte souvent
en première approximation la loi de conduction de Fourier qui de
façon générale s'écrit:
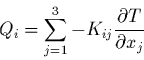 |
(32) |
où le tenseur de conduction thermique 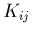 dépend en
général de la température. En fait dans le cas d'un milieu isotrope,
cas des fluides en général :
dépend en
général de la température. En fait dans le cas d'un milieu isotrope,
cas des fluides en général :
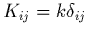 et donc
et donc
 |
(33) |
Dans ce cas, on peut montrer que
le terme de dissipation thermique 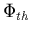 s'écrit:
s'écrit:
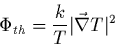 |
(34) |
Cas particulier d'un fluide visqueux, homogène,
incompressible, à chaleur spécifique constante:
Équation de la chaleur
La donnée des coefficients de dissipation  et
et 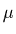 , supposés
généralement constants quand le fluide est incompressible, suffit pour
définir le comportement qui s'écrit
, supposés
généralement constants quand le fluide est incompressible, suffit pour
définir le comportement qui s'écrit
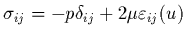 |
|
|
|
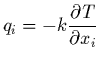 |
|
|
(35) |
La relation d'incompressibilité
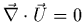 tient lieu de loi d'état car elle implique en
particulier:
tient lieu de loi d'état car elle implique en
particulier: 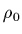 =constante.
Il suffit donc de connaître
=constante.
Il suffit donc de connaître 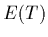 , ou ce qui revient au même, la chaleur
spécifique du fluide. Si elle est constante et égale à
, ou ce qui revient au même, la chaleur
spécifique du fluide. Si elle est constante et égale à 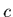 , on a:
, on a:
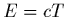 .
.
On a vu que le système d'équations de Navier-Stokes permet la
détermination de 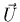 et du gradient de
et du gradient de 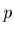 . Les effets thermiques
sont bien ici découplés des effets mécaniques.
En l'absence de source de
chaleur
. Les effets thermiques
sont bien ici découplés des effets mécaniques.
En l'absence de source de
chaleur 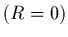 , l'équation de l'énergie (30) s'écrit,
compte-tenu des relations précédentes:
, l'équation de l'énergie (30) s'écrit,
compte-tenu des relations précédentes:
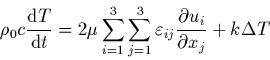 |
(36) |
soit
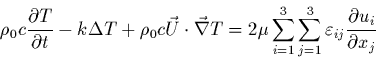 |
(37) |
moyennant des conditions initiales et aux limites adaptées (notamment du
type de (31)), cette relation
permet de déterminer 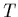 lorsque
lorsque  est préalablement calculé par
résolution de Navier-Stokes.
est préalablement calculé par
résolution de Navier-Stokes.
Dans le cas particulier d'un fluide parfait (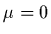 ) et si l'on peut
faire une hypothèse de petites perturbations (faibles vitesses et faibles
gradients de température), l'équation précédente se réduit à
l'équation dite de la chaleur, qui est du même type
mathématique que les équations de diffusion visqueuse (22)
déjà évoquées précédemment:
) et si l'on peut
faire une hypothèse de petites perturbations (faibles vitesses et faibles
gradients de température), l'équation précédente se réduit à
l'équation dite de la chaleur, qui est du même type
mathématique que les équations de diffusion visqueuse (22)
déjà évoquées précédemment:
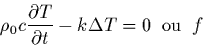 |
(38) |
s'il existe une source de chaleur volumique 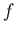 .
.


Next: 0.3 Élasticité linéaire
Up: 0.2 Transmission de la
Previous: 0.2.2 Conservation de l'énergie
Michel Moncuquet
DESPA, Observatoire de Paris
2001-03-05
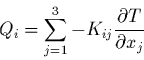
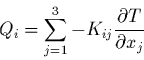
![]() et
et ![]() , supposés
généralement constants quand le fluide est incompressible, suffit pour
définir le comportement qui s'écrit
, supposés
généralement constants quand le fluide est incompressible, suffit pour
définir le comportement qui s'écrit
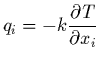
![]() et du gradient de
et du gradient de ![]() . Les effets thermiques
sont bien ici découplés des effets mécaniques.
En l'absence de source de
chaleur
. Les effets thermiques
sont bien ici découplés des effets mécaniques.
En l'absence de source de
chaleur ![]() , l'équation de l'énergie (30) s'écrit,
compte-tenu des relations précédentes:
, l'équation de l'énergie (30) s'écrit,
compte-tenu des relations précédentes:
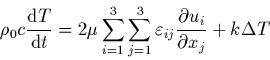
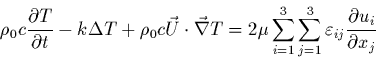
![]() ) et si l'on peut
faire une hypothèse de petites perturbations (faibles vitesses et faibles
gradients de température), l'équation précédente se réduit à
l'équation dite de la chaleur, qui est du même type
mathématique que les équations de diffusion visqueuse (22)
déjà évoquées précédemment:
) et si l'on peut
faire une hypothèse de petites perturbations (faibles vitesses et faibles
gradients de température), l'équation précédente se réduit à
l'équation dite de la chaleur, qui est du même type
mathématique que les équations de diffusion visqueuse (22)
déjà évoquées précédemment: