| (16) | |||
Dans un écoulement stationnaire, le problème de Navier-Stokes est
réduit à:
Écoulement stationnaire irrotationnel d'un fluide parfait incompressible
On considère l'écoulement engendré par un obstacle solide
indéformable au sein d'un fluide parfait incompressible, et on
suppose le champ de vitesse irrotationnel (ou si l'on préfère on ne
s'intéresse qu'à la partie irrotationnel de l'écoulement). Dans ce
cas, il existe un potentiel ![]() tel que
tel que
![]() ;
; ![]() ne dépendant que de la position
ne dépendant que de la position
![]() dans le cas stationnaire. Toujours dans ce cas
dans le cas stationnaire. Toujours dans ce cas ![]() extérieur
de l'obstacle) est non borné et
extérieur
de l'obstacle) est non borné et ![]() est la paroi de l'obstacle.
est la paroi de l'obstacle.
L'incompressibilité d'une part et les conditions aux limites de
(18) d'autre part se traduisent alors par :
 |
(19) |
Écoulement stationnaire d'un fluide visqueux incompressible dans une conduite cylindrique
C'est un problème classique à une dimension. Des pressions ![]() et
et
![]() constantes sont imposées respectivement aux deux extrémités de
la conduite de grande longueur
constantes sont imposées respectivement aux deux extrémités de
la conduite de grande longueur ![]() et l'on suppose que les forces volumiques
extérieures (poids du liquide) sont
négligeables par rapport au gradient de pression (i.e.
et l'on suppose que les forces volumiques
extérieures (poids du liquide) sont
négligeables par rapport au gradient de pression (i.e. ![]() ).
On modélise la conduite par un cylindre infini et l'on remplace alors
les données effectives
).
On modélise la conduite par un cylindre infini et l'on remplace alors
les données effectives ![]() et
et ![]() par celle de la chute
linéique de pression
par celle de la chute
linéique de pression ![]() définie par
définie par
![]() .
.
On cherche alors une vitesse ![]() (dans la direction du tuyau, les
autres composantes étant nulles) solution
du problème de Navier-Stokes 17 qui se réduit alors à:
(dans la direction du tuyau, les
autres composantes étant nulles) solution
du problème de Navier-Stokes 17 qui se réduit alors à:
![]() , les autres dérivées
partielles de
, les autres dérivées
partielles de ![]() étant nulles.
étant nulles. ![]() ne dépend donc que de
ne dépend donc que de ![]() ,
cependant que
,
cependant que ![]() ne dépend que de
ne dépend que de ![]() et
et ![]() (identiquement),
on a donc
(identiquement),
on a donc
![]() constante
constante ![]() .
.
Finalement, compte-tenu de la condition d'adhérence de (17),
le problème se réduit à chercher la vitesse d'écoulement ![]() en fonction
de la distance
en fonction
de la distance ![]() au centre de la conduite en résolvant l'équation
différentielle ordinaire:
au centre de la conduite en résolvant l'équation
différentielle ordinaire:
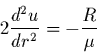 |
(21) |
Écoulement plan stationnaire d'un gaz parfait barotrope
Nous nous intéressons ici à la perturbation (supposée petite) d'un
écoulement uniforme par on obstacle cylindrique, de longueur supposée
infinie, dont l'axe est perpendiculaire à la direction de l'écoulement.
Le fluide est supposé parfait et compressible barotrope. On choisit
la section droite de l'obstacle comme plan ![]() .
.
Soit donc
![]() la vitesse uniforme de l'écoulement
avant perturbation (
la vitesse uniforme de l'écoulement
avant perturbation (![]() est choisi parallèle à
est choisi parallèle à
![]() et
et ![]() est le module de cette vitesse. On note
est le module de cette vitesse. On note
![]() et
et ![]() les masse volumique,
pression et vitesse du son du fluide initial.
La quantité
les masse volumique,
pression et vitesse du son du fluide initial.
La quantité
![]() est appelé le nombre de
Mach de l'écoulement non perturbé.
est appelé le nombre de
Mach de l'écoulement non perturbé.
On définit la perturbation à l'aide d'un paramètre «infiniment petit»
noté ![]() dont
la signification physique (à préciser dans chaque cas à traiter) est
liée ici au fait que
dont
la signification physique (à préciser dans chaque cas à traiter) est
liée ici au fait que ![]() est grand et l'obstacle est petit par rapport
au domaine «sans limite» dans lequel il est plongé. Les grandeurs
caractérisant l'écoulement perturbé sont alors:
est grand et l'obstacle est petit par rapport
au domaine «sans limite» dans lequel il est plongé. Les grandeurs
caractérisant l'écoulement perturbé sont alors:
![]() .
.
La
linéarisation du système d'Euler stationnaire (18), conduit
alors au système :
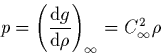 |
(26) |
| (27) |
La condition aux limites naturelle sur l'obstacle, puisque le fluide est
parfait, est une condition de glissement de type (14) sur la
frontière ![]() de l'obstacle. Cette condition doit être aussi
linéarisée
et s'explicite au cas par cas, ce qu'on ne fera pas ici.
Notons seulement que ces conditions de glissement se traduirons par des
conditions en
de l'obstacle. Cette condition doit être aussi
linéarisée
et s'explicite au cas par cas, ce qu'on ne fera pas ici.
Notons seulement que ces conditions de glissement se traduirons par des
conditions en ![]() donc en dérivées premières de
donc en dérivées premières de ![]() sur la
frontière
sur la
frontière ![]() de l'obstacle.
de l'obstacle.
En bilan, l'écoulement perturbé est donc déterminé à partir
du potentiel ![]() , solution de (28), avec
, solution de (28), avec
![]() à
l'infini, moyennant
des conditions sur les dérivées premières de
à
l'infini, moyennant
des conditions sur les dérivées premières de ![]() sur
sur ![]() .
Une fois
.
Une fois ![]() calculé, on en déduit:
calculé, on en déduit:
| (29) |